ЧАСТЬ I: СГЛАЖИВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ
Основные шаги этой обучающей программы, которым мы будем следовать:Хорошая стратегия на поверхности, которая имеет едва заметное искривление, подобно этой, состоит в том, чтобы использовать некоторые из линий теоретических шпангоутов, сделать их простыми кривыми в Rhino и затем создать через них поверхность по сечениям.
1 Копируйте линии теоретических шпангоутов, по которым мы должны строить поверхность, сохраняя существующие линии, чтобы проверить заключительную поверхность.
2 Используйте Rhino для автоматического сглаживания и реконструкции кривых в простые кривые.
3 Вручную сгладьте теоретические шпангоуты и их связь на другие линии теоретических шпангоутов.
4 Удлините и копируйте линии, чтобы закончить линии для простой поверхности.
5 Создайте по сечениям поверхность корпуса.
6 Редактируйте поверхность для сглаживания и формирования кромок.
7 Обрежьте поверхность по кромкам, чтобы получить желательные кромки.
Копируйте линии, необходимые для создания поверхности
1 Откройте модель Fairing.3dm.
2 На слое Designer curves выполните команду Copy с опцией InPlace, чтобы дублировать линии теоретических шпангоутов надводного борта, кривые ширстрека и скулы.
3 Измените слой для этих кривых на Surface curves.

Кривые с теоретического чертежа.
4 Выключите слой Designer curves.
5 Имеется намного больше кривых, чем нам необходимо, поэтому удалите примерно половину теоретических шпангоутов.
В областях, где имеются незначительные изменение формы от одной кривой к следующей, Вы можете удалить больше кривых чем в тех областях, где имеются больше изменения. На приведённом ниже рисунке показаны оставшиеся кривые.
Вы можете удалить два из каждых трех теоретических шпангоута в в кормовой части и каждый второй теоретический шпангоут ближе к носу.

Кривые, необходимые для создания поверхности.
Теперь Вы готовы начать сглаживание этих кривые.
Сглаживание простых кривых
Кривые имеют в Rhino две характеристики: число контрольных точек и степень. Степень определяется, как каждая из контрольных точек влияет на кривую.
Мы заинтересованы в простых кривых, созданными из единственного полиномиального интервала. Простые кривые имеют самые гладкие из возможных кривые и делают очень простые поверхности, которые легко редактировать.
Чтобы делать простые кривые в Rhino, создайте кривые, которые имеют число контрольных точек на единицу больше, чем степень кривой. Кривая 1-ой степени (прямая линия) нуждается только в двух контрольных точках; кривая 2-ой степени нуждается только в трех контрольных точках; кривая 3-й степени нуждаются только в четырех контрольных точках, кривая 4-ой степени нуждается только в пяти контрольных точках и кривая 5-ой степени нуждаются только в шести контрольных точках. Если Вы находите, что нуждаетесь в больше чем шести контрольных точках, Вы вероятно пробуете некоторое чрезвычайное сглаживание, что делает сглаживание возможным, но намного боле трудоёмким. Держите эту идею простой кривой в уме, по мере того как мы можем посмотреть кривые на корпусе.
Анализ кривых корпуса
Выделите несколько теоретических шпангоутов и включите отображение эпюры кривизны. Как Вы можете видеть, кривые не являются гладкими. Они имеют очень плотные эпюры кривизны, которые извиваются взад-вперёд.
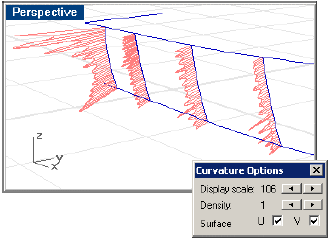
Кривизна кривых корпуса
Сглаживание кривых
Для сглаживания этих кривых сначала определите, какое количество точек потребуется для каждой кривой. Это некоторые общие правила для определения необходимого числа точек:
• Если кривая должна быть прямой линией, используйте две контрольные точки.
• Если изгиб только в одном направлении (c-форма) и Вы должны контролировать только где и насколько изменяется форма кривой, Вы нуждаетесь в кривой 3-ей степени с четырьмя контрольными точками.
• Если кривая имеет s-форму, полностью изменяя искривление в середине кривой, Вы нуждаетесь в кривой 5-ой степенями с шестью контрольными точками.
Основываясь на эпюрах кривизны, кривые 3 и 4 изгибаются в двух направлениях из-за перехода от развала борта в носовой части, так что мы реконструируем их в кривые 5-ой степени с шестью контрольными точками. Кривые 1, 2 и 5-9 изгибаются только в одном направлении, поэтому мы реконструируем их в кривые 3-й степени с четырьмя контрольными точками.
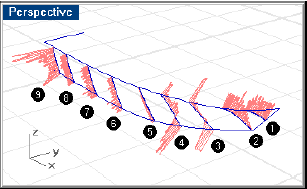
Эпюры кривизны на всех кривых корпуса.
Pages:
- by Admin
- posted at 10:02 дп
- 23 апреля, 2012
Add comment